Cette page explique comment le service Open Street utilise des outils mathématiques, notamment la théorie des graphes, afin de décrire les problématiques du voyageur de commerce qui se cachent derrière chaque calcul d’optimisation.
Elle permet de modéliser, puis ensuite de résoudre les problèmes tels que vous les entrez dans notre service ou nos API. Prenons l’exemple d’un trajet devant passer par Paris, Marseille, Lyon et Toulouse.
Ce trajet à quatre villes est l’exemple le plus simple possible, que l’on peut décrire par un graphe composé de nœuds et de liens. Ici les nœuds sont représentés en disques bleu et les liens en traits noirs.
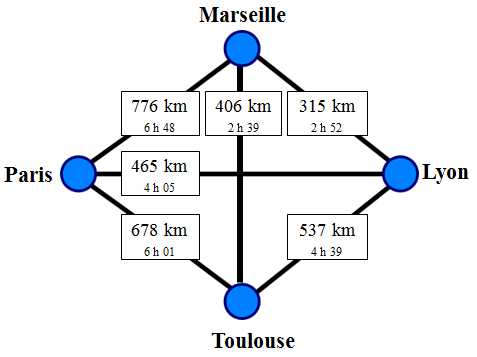
Graphe avec 4 points
Le graphe ci-dessus est très simplifié car en pratique, tous les liens sont doubles. En effet, la distance entre Paris et Toulouse n’est pas exactement la même que celle entre Toulouse et Paris en raison principalement des sens interdits et des bretelles d’autoroute asymétriques. On dit dans ce cas que le graphe est « orienté ».
Ainsi, la combinatoire indique qu’il existe 24 possibilités différentes de parcours. En fixant une ville comme point de départ, ce chiffre descend à 6.

Combinaisons possibles pour le problème du voyageur de commerce
Pour un nombre de villes si restreint, on peut facilement visualiser ces 6 possibilités. C’est un tableau de 6 par 4.
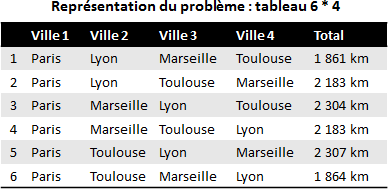
Tableau des possibilités illustrant le problème du voyageur de commerce
A présent, portons à 40 le nombre de villes à visiter. Le graphe correspondant contiendrait 40 nœuds reliés les uns aux autres par des liens à double sens. La combinatoire indique que le nombre de possibilités différentes pour effectuer ce parcours est astronomique. Il y en a en effet 203 978 820 811 97 443 358 640 281 739 902 897 356 800 000 000.

La factorielle permet de calculer le nombre d’itinéraires possibles pour une optimisation (ici de 40 points)
La représentation sous forme de tableau contiendrait 40 colonnes et 2 1046 lignes. La comparaison de toutes ces possibilités par l’ordinateur le plus puissant du monde prendrait des siècles. En pratique, elle est impossible à partir de quelques dizaines de villes seulement.
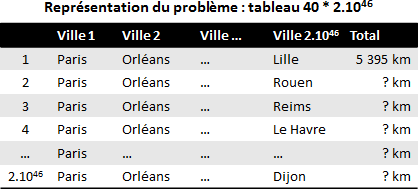
Tableau des possibilités pour une optimisation de 40 points
Le service Open Street permet cependant d’optimiser des itinéraires jusqu’à plusieurs milliers de villes. Vous vous en douterez, nous n’essayons pas de comparer tous les itinéraires possible, mais utilisons des algorithmes bien plus élaborés dont nous pouvons vous faire bénéficier.
